Getaran adalah gerakan bolak-balik dalam suatu interval waktu tertentu. Getaran berhubungan dengan gerak osilasi benda dan gaya yang berhubungan dengan gerak tersebut. Semua benda yang mempunyai massa dan elastisitas mampu bergetar, jadi kebanyakan mesin dan struktur rekayasa (engineering) mengalami getaran sampai derajat tertentu dan rancangannya biasanya memerlukan pertimbangan sifat osilasinya.
Pentingnya Belajar Getaran Mekanik
- Salah satu tujuan belajar getaran adalah mengurangi efek negatif getaran melalui desain mesin yang baik
- Hampir semua alat gerak mempunyai masalah getaran karena adanya ketidak seimbangan mekanisme, contohnya :
- Mechanical failures karena material fatigue
- Getaran dapat mengakibatkan keausan yang lebih cepat
- Dalam proses manufaktur, getaran dapat menyebatkan hasil akhir yang buruk
- Selain efek yang merusak, getaran dapat digunakan untuk hal hal yang berguna.
- Getaran digunakan dalam conveyors getar, mesin cuci, sikat gigi elektrik.
- Getaran juga digunakan dalam pile driving, vibratory testing of materials.
- Getaran digunakan untuk menaikan efisiensi dari proses permesinan seperti casting dan forging.
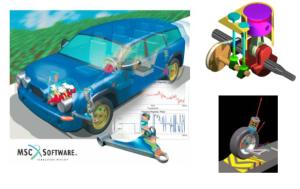
Mekanisme getaran pada mobil
Pengelompokkan Getaran
- Getaran Bebas dan Paksa
- Getaran Teredam dan tak teredam
- Getaran Deterministic dan Random
1. Getaran Bebas Dan Getaran Paksa
Getaran Bebas
Getaran bebas terjadi jika sistem berosilasi karena bekerjanya gaya yang ada dalam sistem itu sendiri (inherent), dan jika ada gaya luas yang bekerja. Sistem yang bergetar bebas akan bergerak pada satu atau lebih frekuensi naturalnya, yang merupakan sifat sistem dinamika yang dibentuk oleh distribusi massa dan kekuatannya. Semua sistem yang memiliki massa dan elastisitas dapat mengalami getaran bebas atau getaran yang terjadi tanpa rangsangan luar.
Getaran Paksa
Getaran paksa adalah getaran yang terjadi karena rangsangan gaya luar, jika rangsangan tersebut berosilasi maka sistem dipaksa untuk bergetar pada frekuensi rangsangan. Jika frekuensi rangsangan sama dengan salah satu frekuensi natural sistem, maka akan didapat keadaan resonansi dan osilasi besar yang berbahaya mungkin terjadi. Kerusakan pada struktur besar seperti jembatan, gedung ataupun sayap pesawat terbang, merupakan kejadian menakutkan yang disebabkan oleh resonansi. Jadi perhitungan frekuensi natural merupakan hal yang utama.
2. Getaran Teredam dan Tak Teredam
Damping
— Dalam system dynamic bekerja dissipative forces – friction, structural resistances
— Umumnya, damping dalam structural systems adalah kecil dan mempunyai efek yang kecil terhadap natural frekuensi
— Tetapi, damping mempunyai pengaruh yang besar dalam mengurangi resonant pada structural system
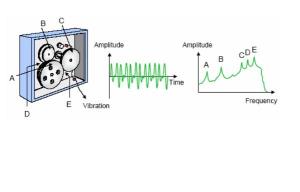
3. Getaran Deterministic dan Random
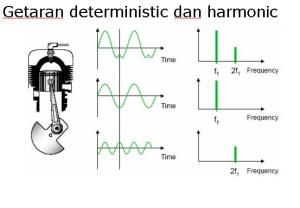
Getaran Deterministic
Sinyal disebut deterministic, selama harga dari sinyal dapat diprediksi.
Getaran deterministic
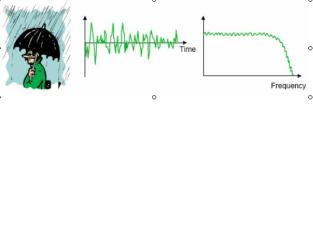
Getaran Random
- Tidak memiliki sinyal yang periodik maupun harmonik
- Harga dari getaran random tidak dapat di prediksi
- Tetapi getaran random bisa di gambarkan secara statistik
Getaran bebas tanpa peredam
Pada model yang paling sederhana redaman dianggap dapat diabaikan, dan tidak ada gaya luar yang memengaruhi massa (getaran bebas).
Dalam keadaan ini gaya yang berlaku pada pegas Fs sebanding dengan panjang peregangan x, sesuai dengan hukum Hooke, atau bila dirumuskan secara matematis:
dengan k adalah tetapan pegas.
Sesuai Hukum kedua Newton gaya yang ditimbulkan sebanding dengan percepatanmassa:
Karena F = Fs, kita mendapatkan persamaan diferensial biasa berikut:

Gerakan harmonik sederhana sistem benda-pegas. Bila kita menganggap bahwa kita memulai getaran sistem dengan meregangkan pegas sejauh A kemudian melepaskannya, solusi persamaan di atas yang memerikan gerakan massa adalah:
Solusi ini menyatakan bahwa massa akan berosilasi dalamgerak harmonis sederhana yang memiliki amplitudo A dan frekuensi fn. Bilangan fn adalah salah satu besaran yang terpenting dalam analisis getaran, dan dinamakan frekuensi alami takredam. Untuk sistem massa-pegas sederhana, fndidefinisikan sebagai:
Catatan: frekuensi sudut ω (ω = 2πf) dengan satuan radian per detik kerap kali digunakan dalam persamaan karena menyederhanakan persamaan, namun besaran ini biasanya diubah ke dalam frekuensi “standar” (satuan Hz) ketika menyatakan frekuensi sistem.
Bila massa dan kekakuan (tetapan k) diketahui frekuensi getaran sistem akan dapat ditentukan menggunakan rumus di atas.
Getaran bebas dengan redaman
 Bila peredaman diperhitungkan, berarti gaya peredam juga berlaku pada massa selain gaya yang disebabkan oleh peregangan pegas. Bila bergerak dalam fluida benda akan mendapatkan peredaman karena kekentalan fluida. Gaya akibat kekentalan ini sebanding dengan kecepatan benda. Konstanta akibat kekentalan (viskositas) c ini dinamakan koefisien peredam, dengan satuan N s/m (SI)
Bila peredaman diperhitungkan, berarti gaya peredam juga berlaku pada massa selain gaya yang disebabkan oleh peregangan pegas. Bila bergerak dalam fluida benda akan mendapatkan peredaman karena kekentalan fluida. Gaya akibat kekentalan ini sebanding dengan kecepatan benda. Konstanta akibat kekentalan (viskositas) c ini dinamakan koefisien peredam, dengan satuan N s/m (SI)
Dengan menjumlahkan semua gaya yang berlaku pada benda kita mendapatkan persamaan
Solusi persamaan ini tergantung pada besarnya redaman. Bila redaman cukup kecil, sistem masih akan bergetar, namun pada akhirnya akan berhenti. Keadaan ini disebut kurang redam, dan merupakan kasus yang paling mendapatkan perhatian dalam analisis vibrasi. Bila peredaman diperbesar sehingga mencapai titik saat sistem tidak lagi berosilasi, kita mencapai titik redaman kritis. Bila peredaman ditambahkan melewati titik kritis ini sistem disebut dalam keadaan lewat redam.
Nilai koefisien redaman yang diperlukan untuk mencapai titik redaman kritis pada model massa-pegas-peredam adalah:
Untuk mengkarakterisasi jumlah peredaman dalam sistem digunakan nisbah yang dinamakan nisbah redaman. Nisbah ini adalah perbandingan antara peredaman sebenarnya terhadap jumlah peredaman yang diperlukan untuk mencapai titik redaman kritis. Rumus untuk nisbah redaman (ζ) adalah
Sebagai contoh struktur logam akan memiliki nisbah redaman lebih kecil dari 0,05, sedangkan suspensi otomotif akan berada pada selang 0,2-0,3.
Solusi sistem kurang redam pada model massa-pegas-peredam adalah
Nilai X, amplitudo awal, dan ϕ, ingsutan fase, ditentukan oleh panjang regangan pegas.
Dari solusi tersebut perlu diperhatikan dua hal: faktor eksponensial dan fungsi cosinus. Faktor eksponensial menentukan seberapa cepat sistem teredam: semakin besar nisbah redaman, semakin cepat sistem teredam ke titik nol. Fungsi kosinus melambangkan osilasi sistem, namun frekuensi osilasi berbeda daripada kasus tidak teredam.
Frekuensi dalam hal ini disebut “frekuensi alamiah teredam”, fd, dan terhubung dengan frekuensi alamiah takredam lewat rumus berikut.
Frekuensi alamiah teredam lebih kecil daripada frekuensi alamiah takredam, namun untuk banyak kasus praktis nisbah redaman relatif kecil, dan karenanya perbedaan tersebut dapat diabaikan. Karena itu deskripsi teredam dan takredam kerap kali tidak disebutkan ketika menyatakan frekuensi alamiah
sumber : http://taufiqurrokhman.wordpress.com/2011/07/12/bahan-kuliah-getaran-mekanik/



Tidak ada komentar:
Posting Komentar